- Phase Transitions and Cosparse Tomographic Recovery of Compound Solid Bodies from Few Projections *
 Compared to the well known Nyquist-Shannon sampling theorem, which allows a signal to be accurately reconstructed only if there are twice more measurements available than the sampling rate at which the signal was acquired, compressive sensing (CS) has been advocated as a sparsity promoting approach, able to obtain accurate reconstructions from a few linear, but random and non-adaptive measurements.
Compared to the well known Nyquist-Shannon sampling theorem, which allows a signal to be accurately reconstructed only if there are twice more measurements available than the sampling rate at which the signal was acquired, compressive sensing (CS) has been advocated as a sparsity promoting approach, able to obtain accurate reconstructions from a few linear, but random and non-adaptive measurements.
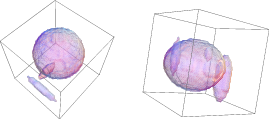
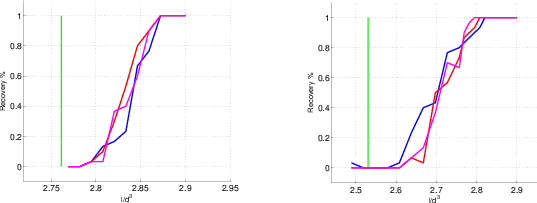
In this paper, we investigate conditions for unique signal recovery based on sparse and cosparse signal models. Moreover, we present a relation between image co-/sparsity and sufficient number of tomographic measurements for exact recovery similar to the settings in CS.
Publication: Denitiu, A.; Petra, S.; Schnörr, Cl. and Schnörr, Ch. Phase Transitions and Cosparse Tomographic Recovery of Compound Solid Bodies from Few Projections. In Fundamenta Informaticae, 135: 73-102, 2014. pdf BibTeX
- An Entropic Perturbation Approach to TV-Minimization for Limited-Data Tomography
We address the problem of reconstructing compound solid bodies from few tomographic projections by regularizing the sparse Anisotropic Total Variation cost function subject to equality constraints, through the addition of a penalized separable nonlinear function. We rely on convex optimization tools, i.e. duality, to reach an objective function that can efficiently be solved using methodologies from unconstrained optimization. Numerical results validate the theory for large-scale recovery problems of integer-valued functions that exceed the capacity of commercial MOSEK software.
Publication: Denitiu, A.; Petra, S.; Schnörr, C. and Schnörr, C. An Entropic Perturbation Approach to TV-Minimization for Limited-Data Tomography. In Discrete Geometry for Computer Imagery (DGCI) 2014, pages 262-274, Springer, LNCS , 2014. pdf BibTeX